LAST UPDATED ON: SEPTEMBER 16, 2024
Banker's Algorithm in Operating System
Banker's algorithm is a deadlock avoidance algorithm. It is named so because this algorithm is used in banking systems to determine whether a loan can be granted or not.
Consider there are n account holders in a bank and the sum of the money in all of their accounts is S. Every time a loan has to be granted by the bank, it subtracts the loan amount from the total money the bank has. Then it checks if that difference is greater than S. It is done because, only then, the bank would have enough money even if all the n account holders draw all their money at once.
Banker's algorithm works in a similar way in computers.
Whenever a new process is created, it must specify the maximum instances of each resource type that it needs, exactly.
Characteristics of Banker's Algorithm
The characteristics of Banker's algorithm are as follows:
-
If any process requests for a resource, then it has to wait.
-
This algorithm consists of advanced features for maximum resource allocation.
-
There are limited resources in the system we have.
-
In this algorithm, if any process gets all the needed resources, then it is that it should return the resources in a restricted period.
-
Various resources are maintained in this algorithm that can fulfill the needs of at least one client.
Let us assume that there are n processes and m resource types.
Data Structures used to implement the Banker’s Algorithm
Some data structures that are used to implement the banker's algorithm are:
1. Available
It is an array of length m. It represents the number of available resources of each type. If Available[j] = k, then there are k instances available, of resource type Rj.
2. Max
It is an n x m matrix which represents the maximum number of instances of each resource that a process can request. If Max[i][j] = k, then the process Pi can request atmost k instances of resource type Rj.
3. Allocation
It is an n x m matrix which represents the number of resources of each type currently allocated to each process. If Allocation[i][j] = k, then process Pi is currently allocated k instances of resource type Rj.
4. Need
It is a two-dimensional array. It is an n x m matrix which indicates the remaining resource needs of each process. If Need[i][j] = k, then process Pi may need k more instances of resource type Rj to complete its task.
Need[i][j] = Max[i][j] - Allocation [i][j]
Banker’s algorithm comprises of two algorithms:
-
Safety algorithm
-
Resource request algorithm
Safety Algorithm
A safety algorithm is an algorithm used to find whether or not a system is in its safe state. The algorithm is as follows:
- Let
Work and Finish be vectors of length m and n, respectively. Initially,
Work = Available
Finish[i] =false for i = 0, 1, ... , n - 1.
This means, initially, no process has finished and the number of available resources is represented by the Available array.
- Find an index i such that both
Finish[i] ==false
Need(i) <= Work
If there is no such i present, then proceed to step 4.
It means, we need to find an unfinished process whose needs can be satisfied by the available resources. If no such process exists, just go to step 4.
- Perform the following:
Work = Work + Allocation(i)
Finish[i] = true
Go to step 2.
When an unfinished process is found, then the resources are allocated and the process is marked finished. And then, the loop is repeated to check the same for all other processes.
- If
Finish[i] == true for all i, then the system is in a safe state.
That means if all processes are finished, then the system is in safe state.
This algorithm may require an order of mxn² operations in order to determine whether a state is safe or not.
Resource Request Algorithm
Now the next algorithm is a resource-request algorithm and it is mainly used to determine whether requests can be safely granted or not.
Let Request(i) be the request vector for the process Pi. If Requesti[j]==k, then process Pi wants k instance of Resource type Rj. When a request for resources is made by the process Pi, the following are the actions that will be taken:
1. If Request(i) <= Need(i), then go to step 2;else raise an error condition, since the process has exceeded its maximum claim.
2. If Request(i) <= Available(i) then go to step 3; else Pi must have to wait as resources are not available.
3. Now we will assume that resources are assigned to process Pi and thus perform the following steps:
Available = Available - Request(i);
Allocation(i) = Allocation(i) + Request(i);
Need(i) = Need(i) - Request(i);
If the resulting resource allocation state comes out to be safe, then the transaction is completed and, process Pi is allocated its resources. But in this case, if the new state is unsafe, then Pi waits for Requesti, and the old resource-allocation state is restored.
Disadvantages of Banker's Algorithm
Some disadvantages of this algorithm are as follows:
-
During the time of Processing, this algorithm does not permit a process to change its maximum need.
-
Another disadvantage of this algorithm is that all the processes must know in advance about the maximum resource needs.
-
This algorithm permits the requests to be provided in constrained time, but for one year which is a fixed period.
Now its time to take a look at the Example of Banker's Algorithm:
Banker's Algorithm Example::
Let us consider the following snapshot for understanding the banker's algorithm:
| Processes |
Allocation
A B C |
Max
A B C |
Available
A B C |
| P0 |
1 1 2 |
4 3 3 |
2 1 0 |
| P1 |
2 1 2 |
3 2 2 |
|
| P2 |
4 0 1 |
9 0 2 |
|
| P3 |
0 2 0 |
7 5 3 |
|
| P4 |
1 1 2 |
1 1 2 |
|
- calculate the content of the need matrix?
- Check if the system is in a safe state?
- Determine the total sum of each type of resource?
Solution:
1. The Content of the need matrix can be calculated by using the formula given below:
Need = Max – Allocation
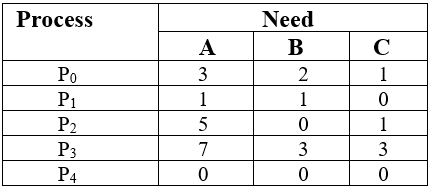
2. Let us now check for the safe state.
Safe sequence:
- For process P0, Need = (3, 2, 1) and
Available = (2, 1, 0)
Need <=Available = False
So, the system will move to the next process.
2. For Process P1, Need = (1, 1, 0)
Available = (2, 1, 0)
Need <= Available = True
Request of P1 is granted.
Available = Available +Allocation
= (2, 1, 0) + (2, 1, 2)
= (4, 2, 2) (New Available)
3. For Process P2, Need = (5, 0, 1)
Available = (4, 2, 2)
Need <=Available = False
So, the system will move to the next process.
4. For Process P3, Need = (7, 3, 3)
Available = (4, 2, 2)
Need <=Available = False
So, the system will move to the next process.
5. For Process P4, Need = (0, 0, 0)
Available = (4, 2, 2)
Need <= Available = True
Request of P4 is granted.
Available = Available + Allocation
= (4, 2, 2) + (1, 1, 2)
= (5, 3, 4) now, (New Available)
6. Now again check for Process P2, Need = (5, 0, 1)
Available = (5, 3, 4)
Need <= Available = True
Request of P2 is granted.
Available = Available + Allocation
= (5, 3, 4) + (4, 0, 1)
= (9, 3, 5) now, (New Available)
7. Now again check for Process P3, Need = (7, 3, 3)
Available = (9, 3, 5)
Need <=Available = True
The request for P3 is granted.
Available = Available +Allocation
= (9, 3, 5) + (0, 2, 0) = (9, 5, 5)
8. Now again check for Process P0, = Need (3, 2, 1)
= Available (9, 5, 5)
Need <= Available = True
So, the request will be granted to P0.
Safe sequence: < P1, P4, P2, P3, P0>
The system allocates all the needed resources to each process. So, we can say that the system is in a safe state.
3. The total amount of resources will be calculated by the following formula:
The total amount of resources= sum of columns of allocation + Available
= [8 5 7] + [2 1 0] = [10 6 7]
Implementation of Banker's Algorithm in C
Given below is the code for Banker's algorithm implementation:
//C program for Banker's Algorithm
#include <stdio.h>
int main()
{
// P0, P1, P2, P3, P4 are the names of Process
int n, r, i, j, k;
n = 5; // Indicates the Number of processes
r = 3; //Indicates the Number of resources
int alloc[5][3] = { { 0, 0, 1 }, // P0 // This is Allocation Matrix
{ 3, 0, 0 }, // P1
{ 1, 0, 1 }, // P2
{ 2, 3, 2 }, // P3
{ 0, 0, 3 } }; // P4
int max[5][3] = { { 7, 6, 3 }, // P0 // MAX Matrix
{ 3, 2, 2 }, // P1
{ 8, 0, 2 }, // P2
{ 2, 1, 2 }, // P3
{ 5, 2, 3 } }; // P4
int avail[3] = { 2, 3, 2 }; // These are Available Resources
int f[n], ans[n], ind = 0;
for (k = 0; k < n; k++) {
f[k] = 0;
}
int need[n][r];
for (i = 0; i < n; i++) {
for (j = 0; j < r; j++)
need[i][j] = max[i][j] - alloc[i][j];
}
int y = 0;
for (k = 0; k < 5; k++) {
for (i = 0; i < n; i++) {
if (f[i] == 0) {
int flag = 0;
for (j = 0; j < r; j++) {
if (need[i][j] > avail[j]){
flag = 1;
break;
}
}
if (flag == 0) {
ans[ind++] = i;
for (y = 0; y < r; y++)
avail[y] += alloc[i][y];
f[i] = 1;
}
}
}
}
printf("Th SAFE Sequence is as follows\n");
for (i = 0; i < n - 1; i++)
printf(" P%d ->", ans[i]);
printf(" P%d", ans[n - 1]);
return (0);
}
Output:
Here is the output of the above program:
![bankers algo output]()
With this we end the banker's algorithm tutorial. We hope you understood it, if not go to our forum and ask your doubt.